近期，37000cm威尼斯物理学院赵宇心课题组在时间反演不变晶体对称性分类中取得重要进展。课题组提出了时间反演不变下晶体对称性投影代数结构分类的基本理论；并将之应用于17种2D空间群，穷举了458种对称性代数结构，为每个空间群设计了"典范模型"，可实现所有可能的代数结构；此外，给出了投影对称性结构导致的超越传统空间群理论的三个新奇物理结果。

对称性是现代物理学最基本的原理之一。1939年，维格纳揭示了，在量子力学中对称群将被投影表示。群的投影表示是指，群乘法运算被相位因子所修正,即ρ(g₁)ρ(g₂)=e^iθ(gz,g2)ρ(g₁,g₂).维格纳将这一原理应用于庞加莱群，给出了基本粒子的分类。庞加莱群是高能物理中的时空群，与之对应，固体物理中的时空群是空间群和时间反演不变性。但一般晶体的教科书中，只涉及晶体对称性的一般表示理论，而不讨论投影表示。原因在于晶体对称性理论是为了研究电子晶体而发展起来的，普通的表示理论对于大多数应用已经足够。 但近年来，人工晶体的尖端技术，包括光子和声学晶体、光晶格中的冷原子和机械周期系统使情况发生了改变——这些人工晶体在晶格上具有可设计的规范通量构型，它们将荷载晶体对称性的投影表示。一个规范场下对称性被投影表示的例子如下图：在每个方格子中施加一定规范通量θ时，平移算符 之间的代数关系将被修改为投影对称代数:L_aL_bL_a^-1L_b^-2=e^iθ.

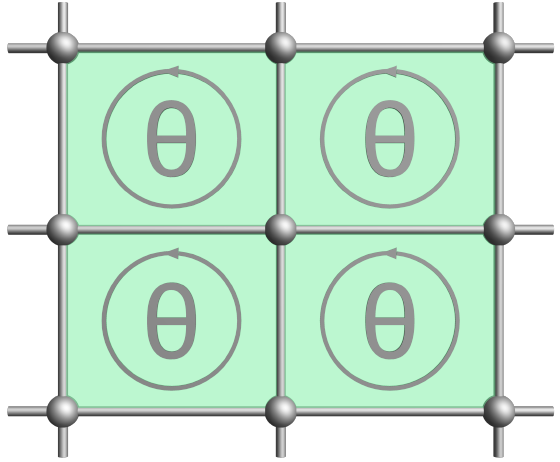
图1：平移对称性在规范场中被投影表示。

近年来，越来越多的研究者认识到，晶体投影对称代数对揭示人造晶体新奇的对称性和拓扑特性至关重要。例如，晶体投影对称代数可导致动量空间的基本域从环面变为克莱因瓶，交换自旋和无自旋系统的拓扑分类，在Hofstadter模型中产生的新拓扑相，实现莫比乌斯绝缘体等等。这些新奇的例子表明，系统地发展晶体投影对称性理论将是非常有用的。

近期，赵宇心课题组提出了时间反演不变下晶体对称性投影代数结构分类的基本理论，并将之系统应用于所有2D空间群，取得如下成果：

•数学上，得到了二维空间群（即17个墙纸群）在时间反演不变规范场下扩展成的458 种Z₂对称投影代数，并以生成元关系的显式表示。（表1）

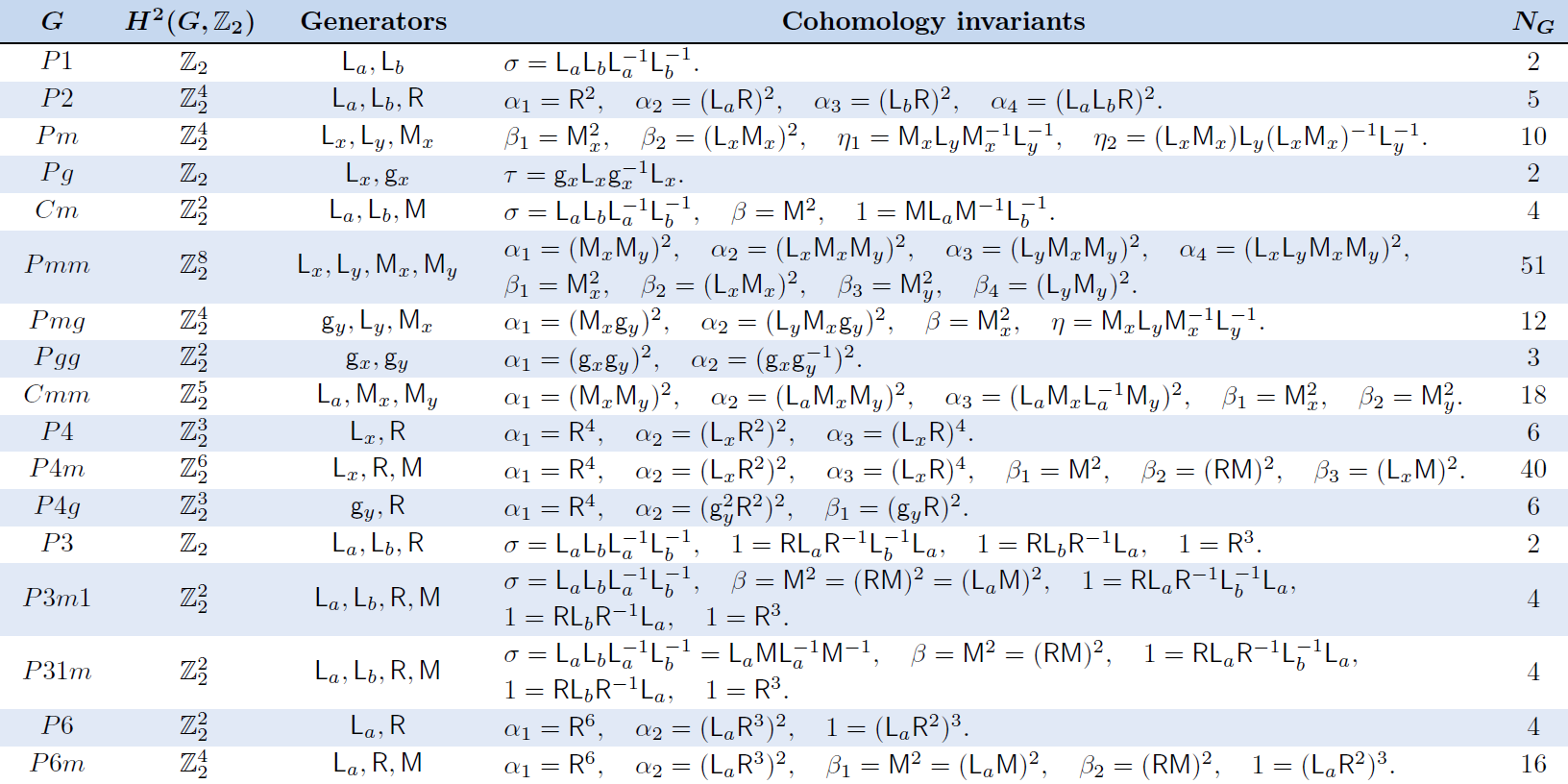
表2：17个墙纸群的所有 投影代数。

• 基于精心选择的投影对称代数的显式表示定义了同调不变量，系统性地揭示了同调不变量与晶体规范构型间的对应关系，使得晶体投影表示可以方便地被物理实现。

• 为所有17个墙纸群构建了"典范模型"（图2）。对于每个墙纸群，典范模型可以实现所有对应的对称投影代数，同一个群的不同投影代数对应于典范模型中的不同的规范通量。因此，对458种对称投影代数都可构建相应的晶体模型。由于物理上的简单性，这些模型都可以通过声学晶体等人工晶体实现。

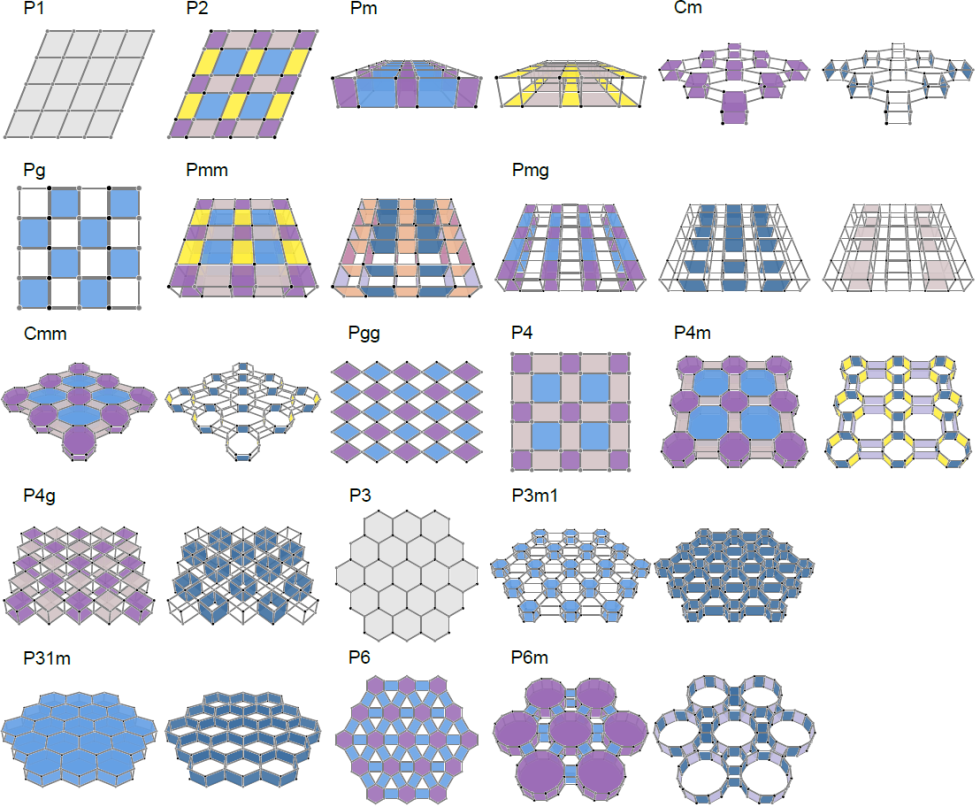
图 2：17个墙纸群的典范模型，每种不同的颜色代表可独立调控规范场通量的区域。

此外，该工作还提出了投影对称性结构导致的超越传统空间群理论的三个新奇物理结果，证明了研究时空投影对称性结构的物理意义。三个新奇结果介绍如下：

投影对称性强制的非平凡Zak相位。在传统理论中，对称性只能保护Zak相。但是投影对称性可以施加更强的约束来强制存在非平凡的Zak相位。

2D投影晶体对称性导致的无自旋 8重简并节点，高于任何已知2D无自旋普通晶体对称性导致的简并。

高对称动量点的重新分布。 在普通的晶体对称理论中，高对称点位于布里渊区的中心或边界上，而对于投影晶体对称性，高对称点可以出现在布里渊区的非中心点处。

该工作以"Classification of time-reversal-invariant crystals with gauge structures"为题发表在 Nature communications [Nat.Comm.14,743(2023)]。论文的第一作者为37000cm威尼斯博士生陈至奕，通讯作者为赵宇心教授，其他作者包括博士生张正和新加坡科技与设计大学杨声远教授。研究受到国家自然科学基金，江苏省基础研究计划，新加坡教育部学术研究基金的支持，在此表示感谢。

该工作的意义在于为晶体投影对称性及其物理实现建立了一套一般性的理论框架，从而为进一步探索规范场下晶体可能具有的新奇物理特性奠定了理论基础。值得一提的是，近年来，赵宇心教授课题组潜心投影对称性的研究，已取得系列创新成果，其它代表性工作包括：提出投影对称性可约化动量空间为克莱因瓶[Nat. Comm. 13, 2215 (2022)]；投影对称性可导致实现新奇拓扑相的新机制[Phys. Rev. Lett. 127, 076401 (2021)];投影对称性可交换有无自旋系统的拓扑分类[Phys. Rev. Lett. 126, 196402 (2021)]。

文章连接：https://www.nature.com/articles/s41467-023-36447-7。