近期，37000cm威尼斯物理学院赵宇心课题组发现，在合适的规范场构型下，空间群的投影表示可以导致动量空间的非简单对称性(nonsymmorphic symmetry)，从而产生超越传统布洛赫理论的新物理。一个有趣的例子是，存在动量空间的滑移镜面对称性(glide reflection symmetry)，可以将拓扑类型为环面的布里渊区约化为克莱因瓶，在这个不可定向流形上可以产生新的Z₂拓扑相。

图 1 规范场导致的布里渊克莱因瓶。下层格点展示规范场通量的分布，上面是动量空间的基本单元——克莱因瓶。

在研究固体材料中发展出的传统能带理论是基于晶体空间群表示理论的。空间群平移子群的傅里叶变换定义了倒格矢，倒格矢下平移等价的动量点的集合构成了布里渊区，其中的布洛赫波矢和平移子群的不可约表示构成了一对一的关系。空间群除以平移子群得到的点群作用在布里渊区上，保持布里渊区的中心也就是Γ点不变。因此，传统能带理论中，空间群在动量空间的作用总是简单的，即点群的操作不含分数的倒格矢平移。即使是实空间中的非简单空间群，其对应的点群在动量空间的操作也是简单的，实空间中格矢的分数平移在动量空间中表现为点群元素操作在布洛赫波函数上的相位因子。

近年来，3D打印技术带来了人工晶体的快速发展，例如声子晶体和光子晶体。相比真实的晶体，人工晶体可以自由设计Z₂范场的分布，即格点上实数跃迁幅的正负号分布可以任意控制和排布。考虑了规范场分布后，晶体对称性满足投影表示，其代数结构会因此改变，从而超越传统的空间群理论，修正传统能带理论中的基本概念。文章[Nat.Comm.13,2215(2022)]指出，在合适的规范场分布下，空间对称性可以在动量空间中表现为带分数倒格矢平移的非简单操作。一个重要的例子是，Z₂规范场分布可以导致为x坐标取逆的镜面对称性M_x与y方向的平移对称性L_y反对易:

{M_x,L_y}=0.

反对易关系导致在动量空间M_x除了要把K_x变为-K_x,还要把K_y平移半个倒格矢,即变为K_y+G_y/2。如此，实空间镜面对称性作为实空间的简单对称性在动量空间变为了非简单的滑移镜面对称性。

与简单空间对称性相比，非简单对称性的作用是自由的(free action)，也就是没有不动点。从拓扑分类的角度讲，一个流形上的具有自由作用对称性约束的拓扑分类等价于对称性约化后流形上无对称性约束的拓扑分类。因此布里渊区作为环面可被滑移镜面对称性进一步约化为克莱因瓶（见图2）。作为不可定向流形，克莱因瓶上最基本的拓扑分类是Z₂型的，区别于环面上的Z型拓扑分类。

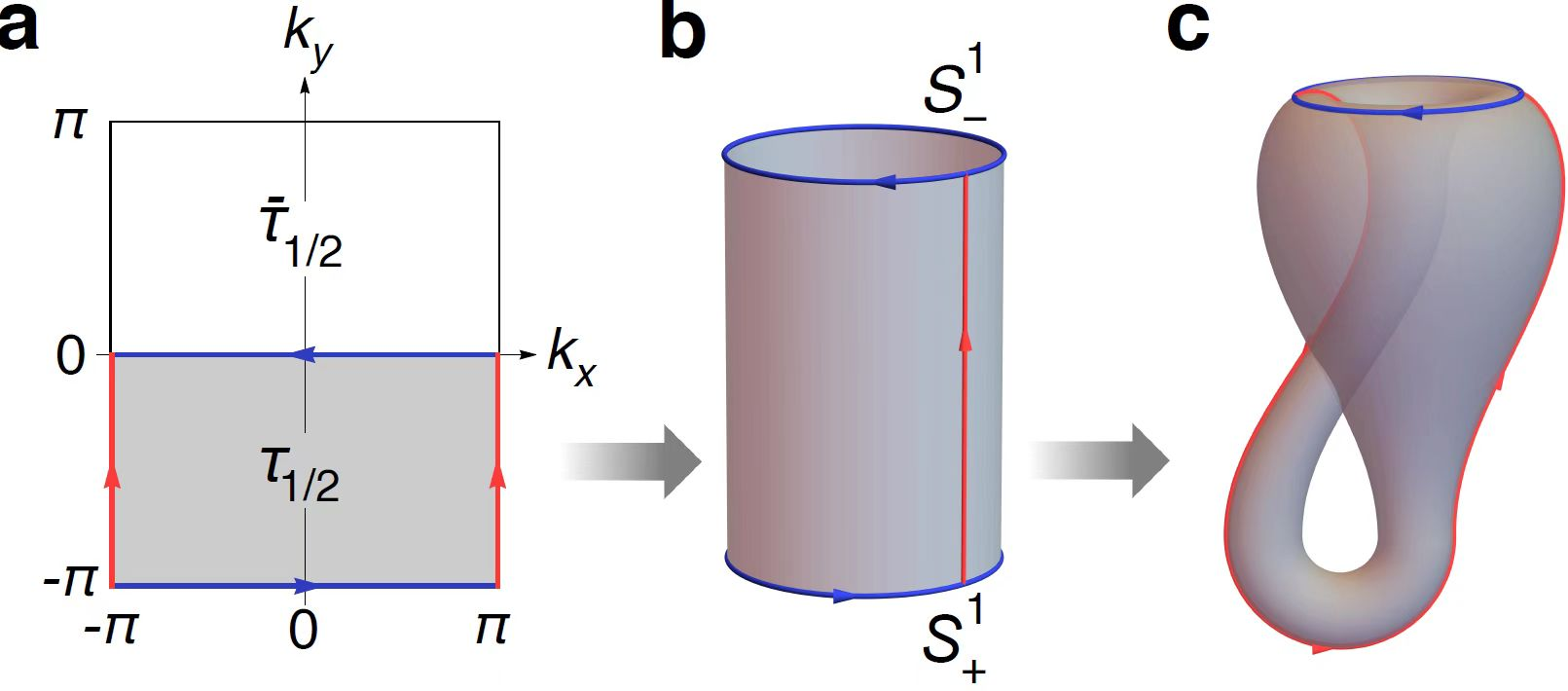
图 2动量空间的滑移镜面对称性及其约化的克莱因瓶。a. 对称性约化下一半布里渊区的边界条件。b. 施加红色周期边界条件导致的圆柱面。c. 进一步施加蓝色反周期边界条件导致的克莱因瓶。

文章进一步研究了克莱因瓶上的拓扑绝缘体。区别于传统的镜面对称性保护的拓扑绝缘体，其保持镜面对称的边界没有带间表面态，表面态反而出现在不保持镜面对称性的边界上。

  值得一提的是，这个工作是37000cm威尼斯赵宇心课题组一系列关于规范场拓展的晶体能带理论中的一个。课题组之前在这个领域的工作包括：1.提出利用规范场交换有无自旋系统PT对称性下拓扑分类的理论^[2]；2.发展了规范场拓展下的k·p方法并用于新奇拓扑相的寻找^[3]；3.提出了平移对称性投影表示导致的新奇拓扑相^[4]。关于Z₂规范场下投影对称性导致的新奇拓扑物态的基本想法和简单模型最近在声学晶体中得到实验验证^[5],并被美国物理学会Physics杂志选为viewpoint介绍^[6]。

该工作相关研究成果以“Brillouin Klein bottle from artificial gauge fields”为题发表为[Nat.Comm.13,2215(2022)]。论文的第一作者为37000cm威尼斯博士生陈至奕，通讯作者为赵宇心教授，其他作者包括新加坡科技与设计大学扬声远教授。研究受到国家自然科学基金委面上项目和国际合作项目的资助，在此表示感谢。

参考文献：

1. Chen, Yang, Zhao*, Nat.Comm.13,2215(2022)

2. Zhao*, Chen, Sheng, and Yang, Phys. Rev. Lett. 126, 196402 (2021)

3. Shao, Liu, Xiao, Yang, Zhao*，Phys. Rev. Lett. 127, 076401 (2021)

4. Zhao*, Huang, Yang, Phys. Rev. B 102, 161117 (2020)

5. Xue, ..., Zhao*, Yang*, Zhang*, Phys. Rev. Lett. 128, 116802 (2022); Li et al, Phys. Rev. Lett. 128, 116803 (2022)

6. Deng and Jing, Physics 15, 36 (2022)

文章连接为：https://www.nature.com/articles/s41467-022-29953-7