近期，37000cm威尼斯现代工程与应用科学学院李涛、祝世宁研究组在拓扑光子态调控方面取得系列进展。他们在理论和实验上首次发现了由Floquet人工规范场相变诱导产生的拓扑模式，通过合理的Floquet规范场设计，可以实现非对称的光局域传输功能。另一方面，他们在非厄米的Floquet体系中发现，通过PT对称的增益/损耗调制可以调控体系的拓扑相变，进一步演示了由非厄米效应诱导产生的Floquet拓扑边界模式。

左图：人工规范场相变诱导产生拓扑模式示意图。右图：非厄米调控拓扑模式示意图。

近些年，光子拓扑绝缘体所支持的拓扑态受到人们广泛关注，这种拓扑态由于受到拓扑性质保护而表现出鲁棒性，使得器件对结构尺寸的偏差具有一定容忍度，其在大规模、高密度的光子集成芯片中具有巨大潜力。最近，拓扑光子学被拓展到了周期性调制的Floquet体系，这种体系由于受到周期性调制而展示出新颖的特性，例如全新的拓扑模式反常 π mode的发现 [PRL 122, 173901 (2019)]，这种模式表现出与传统静态拓扑体系中的边界态完全不同的特性。另一方面，人们对非厄米体系的研究逐渐深入，发现非厄米参数的引入可以对拓扑体系中的拓扑性质产生一系列新颖有效的调控。例如可以利用非厄米的增益损耗来恢复严格的拓扑零模，进而增强其鲁棒性 [PRL 123, 165701 (2019)]。非厄米拓扑光学的兴起，不仅打开了全新的物理世界大门，还为未来光子集成中对拓扑态的动态调控提供了一系列可能的方案。

在拓扑物理的研究当中，体边对应关系（bulk-edge correspondence）扮演着预言边界态的重要角色，它描述了这样一个事实：通过系统体（bulk）性质定义的拓扑不变量可以预言体系边界（edge）上边界态的存在，具有不同拓扑不变量的两种材料（拓扑相变）的界面处存在拓扑边界态。对于上述的Floquet体系，拓扑不变量Gπ被定义来预言π mode的存在，并且已有理论和实验上证实，具有非零Gπ体系的边界出现了π mode。但是体边对应关系的逆命题的真伪很少被考虑，即：拓扑边界态的出现是否一定需要拓扑相变呢？

创新研究：
1. 人工规范场相变诱导产生拓扑π模式

在一维波导阵列中，Floquet系统可以通过对波导做周期性弯曲调制实现，其中存在两个重要的调控的自由度：弯曲的频率ω和初相φ。前人的研究发现弯曲频率ω可以调节体系的拓扑相，而对初相φ的调制作用没有深入研究。初相φ对应系统的Floquet规范场（Floquet gauge），在第一项工作中[Laser & Photonics Reviews 15, 2000584 (2021)]，研究人员发现，若将两个处在相同拓扑相但不同规范场（即弯曲的频率ω相同而初相φ不同）的波导阵列拼接起来（图1(a)），在中间的界面处就可能出现边界模式。随着规范场差异逐渐增大时，原来平庸的体带模式会逐渐凸显出来，在当两个体系的规范场相差π时（规范场相变），形成两个全新的π模式（图1(b)）。此时，两个拼接的波导阵列虽然处在相同的拓扑相中，但中间的界面仍然支持拓扑π模，在这样的体系中，从界面波导输入的光场可以被局域在波导界面向前传输(图1(c-e))。进一步的研究表明，通过精细地控制拼接的波导阵列在输入和输出端的规范场，可以实现非对称的拓扑传输：即体系只在一个方向上支持局域的光场传输，而从另一端输入的光会弥散到体系当中。研究人员随后硅波导阵列实验中证实了由规范相变而导致的界面π模式，并且观察到了拓扑模式的不对称传输，并且这种不对称传输在近100nm带宽下都展示出很好的非对称特性（图2）。

成功在实验上演示了这种规范场相变诱导产生的拓扑π模之后，研究人员进一步揭示了其背后的物理机理，发现两个Floquet规范相反的体系的哈密顿量由于规范相变而具有相反的Floquet-Dirac质量项。类似于Jackiw-Rebbi模型，这种π能隙质量项的反向会使得Floquet能带反转，从而导致在两个具有不同规范的系统界面上产生边界态（见图3）。

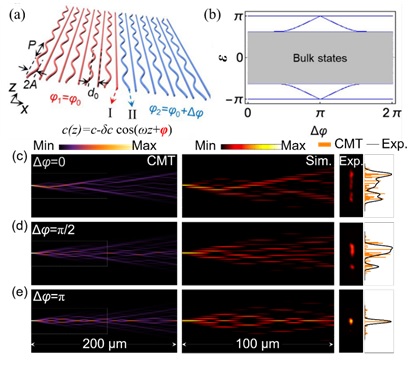
图1. (a) 拓扑相相同而Floquet规范场不同的两个波导阵列形成规范相变界面。(b) Floquet规范差Δφ导致系统准能量ε的变化。(c) 耦合模理论计算、有限元数值模拟和实验观察到的在不同Δφ下的光场演化。

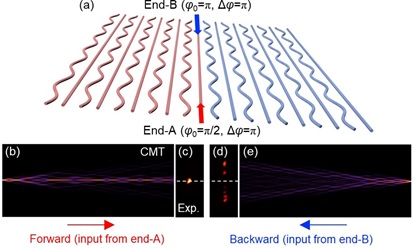
 图2. (a) 非对称拓扑传输波导阵列示意图。理论(b,e)和实验(c,d)中观察到的非对称光场传输行为。

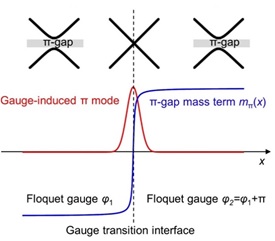
图 3. Floquet规范相变诱导π界面态产生的示意图

2. 非厄米调控Floquet拓扑模式

在另一项工作中，研究人员关注了非厄米的Floquet波导阵列（图4(a)）。研究发现，在一个有限的Floquet体系中，如果向原本处于拓扑平庸的体系添加增益和损耗，可以在带隙中恢复π模式（图4(b)）。实验表明，发现在没有损耗的硅波导阵列中，边界输入的光场会弥散到体系内部；而在添加了损耗（镀Cr）的波导阵列中，边界输入的光会由于π模式恢复而局域在边界进行传输（图4(c,d)）。实验和理论的结果吻合很好，证实了损耗诱导产生的Floquet π模式。

理论上，研究人员计算了非厄米体系下系统的拓扑不变量Gπ，给出了非厄米调控下的拓扑相图。可以看到，在调制频率不变的情况下，通过调节非厄米增益损耗的大小，可以实现体系的拓扑相变过程（图5(a)虚线）。得一提的是，在静态的拓扑体系中，PT对称的增益损耗会压缩能带，从而导致能带闭合。而在动态的Floquet体系中，周期性的调制所导致的多个复制能带在被引入增益损耗压缩的同时，会在不同阶数的复制带间打开带隙，这些带隙即π能隙，正是由于它导致了非厄米Floquet π模式的出现（见图5(c,d)）。这项工作说明可以借由非厄米增益/损耗强度来控制π模式存在，为实现拓扑模式的动态调控提供可能。

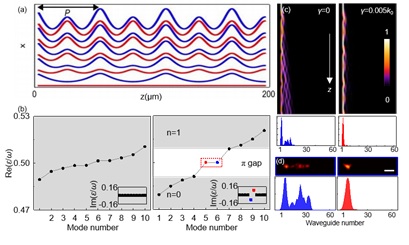
图 4. (a) 非厄米波导阵列示意图。(b) 厄米和非厄米体系的准能量，在非厄米体系打开的π带隙中，出现了两个孤立的模式，即π模式。(c) 理论计算的边界输入光场在厄米和非厄米体系中的演化和出射端归一化能量分布。(d) 实验中CCD拍摄的出射端能量分布及归一化能量分布。

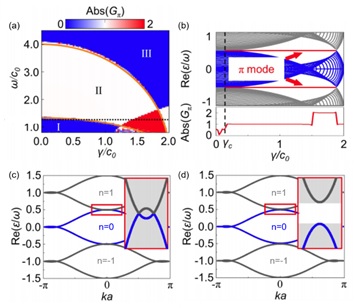
图 5. (a) 拓扑不变量Gπ随频率ω与增益损耗大小γ变化相图。 (b) 系统准能量随增益损耗变化，可以看到带隙中π模式的出现。 (c, d)厄米和非厄米体系能带，厄米体系中本闭合的π带隙(c)由于增益损耗的引入被打开(d)。

相关研究成果分别发表在《Laser & Photonics Reviews》，《Physical Review Research》和《人工晶体学报》上。37000cm威尼斯现代工学院博士生宋万鸽、吴圣杰分别为论文第一作者，37000cm威尼斯的李涛教授为论文的通讯作者。相关研究得到了科技部国家重点研发计划、国家自然科学基金委、37000cm威尼斯登峰人才计划等项目的支持。

文章链接：

 https://onlinelibrary.wiley.com/doi/10.1002/lpor.202000584

 https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.3.023211

 http://rgjtxb.jtxb.cn/CN/10.16553/j.cnki.issn1000-985x.20210609.001