近期，37000cm威尼斯固体微结构物理国家重点实验室、人工功能材料江苏省重点实验室、材料科学与工程系及人工微结构科学与技术协同创新中心的卢明辉教授、刘晓平教授与陈延峰教授的研究团队，与南方科技大学卢海舟教授合作，在全固态声学体系中，首次实验探测到了声学赝自旋的存在，并首次实现了固体声波（弹性波）中的类量子自旋霍尔效应，以及具有“背散射抑制”和“自旋-动量锁定”特性的固体声波边界态传输，在此基础上开发出了一种面向全频段可集成的固体声学传输线。相关工作以“Elastic Pseudospin Transport for Integratable Topological Phononic Circuits”为题于2018年8月6日在线发表于《Nature Communications》（《自然-通讯》）杂志。

图1， 利用弹性波量子自旋霍尔效应实现的具有拓扑保护的固体声学传输线：（a）其具有极低的传输损耗，并完全兼容于各工作频段及各类材料。利用该传输线可以构建片上集成声学的基础元件，例如：具有任意路径及形状的（b）固体声声波导、（c）固体声分路器及（d）具有高品质因子的固体声谐振腔等。

声声学在现代工业文明中发挥着极其重要的作用。作为信息与能量的重要载体，声波可以被用于对时间、空间、频率、相位等诸多物理参量的精密测量、信号处理及逻辑运算。声波的这一应用优势，在固体声波（弹性波）方面显得尤为突出——与流体（如空气与水）中的声波相比，固体声波具有几个重要优势,例如：具有很强的抗干扰能力、极低的传输损耗和极高的信息容量等等。同时，固体声波器件易于集成，从而使其被广泛应用于无线通讯、无源传感、无损检测、地球地质勘探以及正在迅速发展的量子计算、量子通信、声子学等诸多领域。

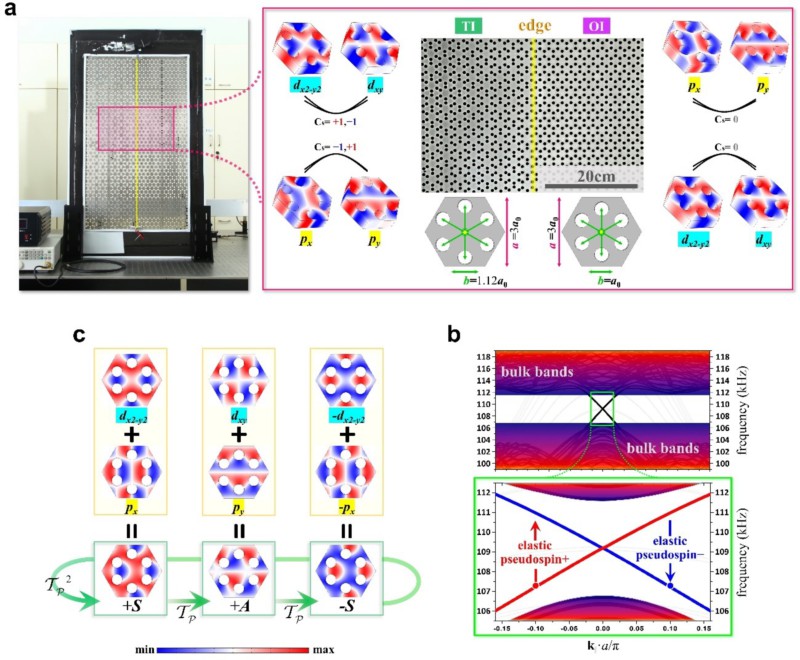
图2，固体声波（弹性波）的赝自旋态的构建：a实验样品由两块固体“声绝缘体”拼接构成，左侧和右侧的“声绝缘体”禁带范围一致，但顶带和底带中的模式互为反转；它们的能带具有不同的拓扑不变量；b由四种简并态构建的赝自旋基矢（S与A）；c拓扑边界态的投影能带：在禁带中存在两条无能隙且具有“自旋-动量锁定”特征的边界模式。

为了进一步释放出固体声波的应用优势，人们迫切地需要一种能够对其进行精确引导和控制的技术手段，即：固体声波的声波导（传输线）。对于光波或是空气中的声波而言，波导的设计及应用已经非常成熟，例如：人们可以利用不同材料间的折射率差异，实现光学波导（如光纤或是片上集成的脊形光波导等）；或是利用不同介质间较大的声阻抗失配，构建空气声的波导（如声波导管等）。然而，实现一个固体声波的波导却一直面临着很大困难。主要原因有下：（一）对于不同的固体材料而言，无论是密度或是弹性模量都很难具有较大的差异，那么通过不同材料间的折射率失配，构建一个具有类似“刚性壁”的声波导就几乎无法实现；（二）固体声波（弹性波）中由于剪切相互作用的存在，声的传播特性对传播介质中的各类缺陷（或转角）极度敏感，这些缺陷很容易导致传输的声波发生较强的散射，从而使得波导内声波的传输能量迅速衰减。上述两点主要困难，使得具有较高传输自由度的“固体声波导”自其概念提出以来一直未能有重要突破。

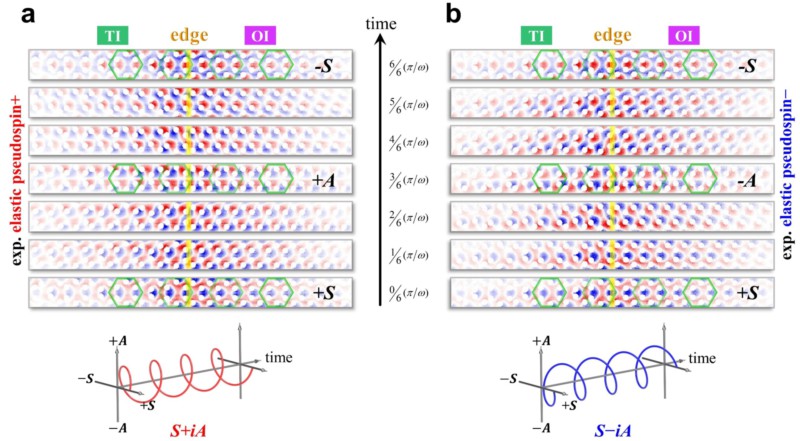
图3，实验探测到的具有“自旋-动量锁定”特征的边界态传输：a由下向上传输的边界态，其固体声波的振动场呈现出“+S→+A→-S→…”的时域特征，对应于一种赝自旋态（S+iA）；b由上向下传输的边界态，其固体声波的振动场呈现出“+S→-A→-S→…”的时域特征，即对应于另一种赝自旋态（S-iA）；弹性波的能量集中于两块绝缘体的边界，并在传输方向的两侧逐渐衰减。

幸运的是，随着近二十年来电子能带拓扑理论和实验研究的蓬勃发展，该体系的核心思想也持续推动了玻色子系统的突破，直接带动了拓扑光子学[1-2]和拓扑声子学[3-4]的迅速发展。人们探索这些拓扑系统的一个重要原因是它们所具有的“无能隙的边界模式”：利用这些受到拓扑保护的边界模式，即可以实现具有“背散射抑制”特性的光或声的“无耗散传输”。这类传输态在不破坏时间反演对称性的情况下，可以免疫各种不同的缺陷（及转角）和杂质，从而使得传输具有了极高的空间自由度和近乎为零的散射损耗。在光学研究中，利用这些拓扑边界模式的优异传输性能，科学家们已经相继提出并实现了一系列前所未有的、面向实际应用的光子集成器件 [5-7]。

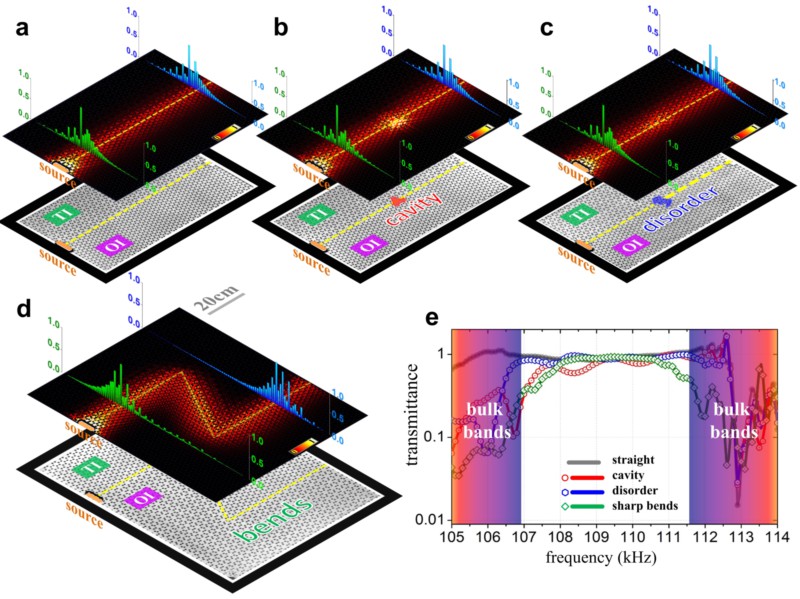
图4，对缺陷及各类转角均免疫的固体声波传输线（波导）：a波导中未放置任何缺陷；b波导中放置一个由15个孔洞缺失构成的“空位”缺陷；c波导中放置一个由15个孔洞随意排布构成的“位错”缺陷；d具有120°大转角的Z型波导；e上述四种波导中固体声波的透过率。数值和实验的结果均表明：固体声波在拓扑边界上的传输没有发生任何背散射，实现了一个传输自由度极高、缺陷免疫、损耗极低且具有较宽工作频段的“完美”固体声波导。

固体声波中的拓扑态（尤其是量子（自旋）霍尔效应），虽然在理论层面已有所预言，如2015年在弹性波体系中提出的利用介质的旋转操作来打破时间反演对称性[8]，或是同年提出的利用具有深亚波长尺度的超构材料来构建出等效赝自旋[9]；但是，由于这些理论设计的限制条件极为苛刻、工程技术难度较大（甚至无法达到），至今无一得到实现。另一方面，迄今所有被实现的拓扑声学系统，都是在仅具有单一自由度的空气声中（纵波）完成的。因此，实现多自由度固体声波的拓扑态不仅能够验证其深刻的物理内涵，在实际应用中也具有非常高的实用价值。

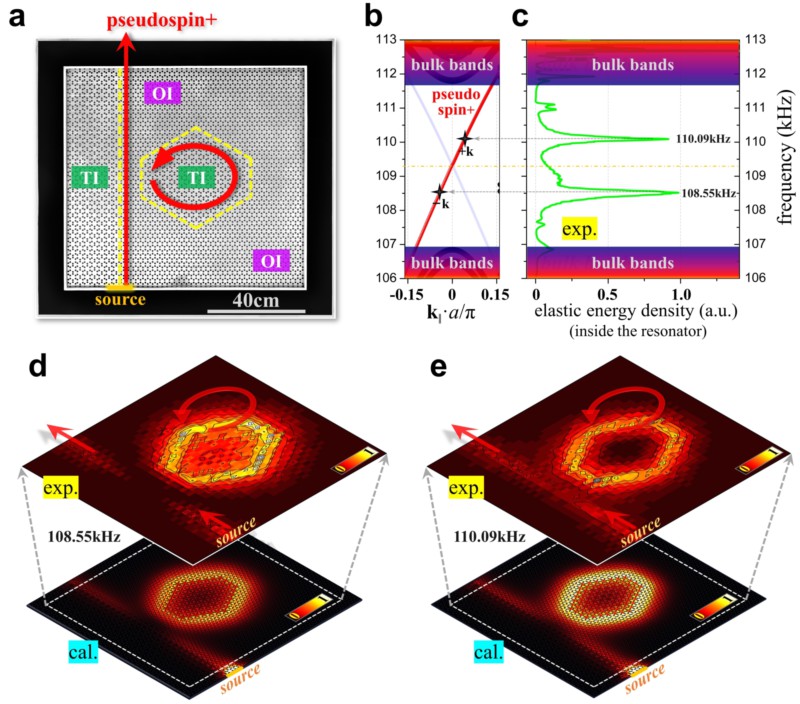
图5，由该固体声波导构建的环形谐振器：a实验样品由（左侧）一根直波导和（右侧）一根闭合六边形波导（环形谐振腔）构成；b固体声波在左侧直波导下端被激发并向上传输，整个系统中仅存在对应于一种“赝自旋”态的传输模式；c实验测量的环形谐振腔中能量频谱，观测到两个的谐振峰（103＜品质因子Q＜104），谐振频率关于边界态的狄拉克点呈对称分布；d和e在这两个谐振频率下，样品中的固体声场分布及能流情况。

基于37000cm威尼斯在人工微结构物理与材料领域的长期研究积累，该研究团队首次提出并成功实现了面向固体声波的（类）量子自旋霍尔效应。实验成功地利用了一种最为简单的结构材料——平板上大小一致的孔洞阵列；经过巧妙设计，这一种材料的固体声波能带具有双重简并的狄拉克点[10,11]，其可被用于构建两个弹性波的赝自旋态，并成功实现了类似于电子系统中的量子自旋霍尔效应。研究团队利用这一固体材料，首次实现了一个几近完美的固体声波导，并通过进一步演化，首次构建了一系列针对固体声波的原型器件：具有极低损耗并可被设计成任意形状的固体声波传输线、固体声波分路器、固体声波谐振腔等等。这一系列具有优异性能特性的固体声波原型器件，为未来实现片上集成声路提供了重要的研究平台。

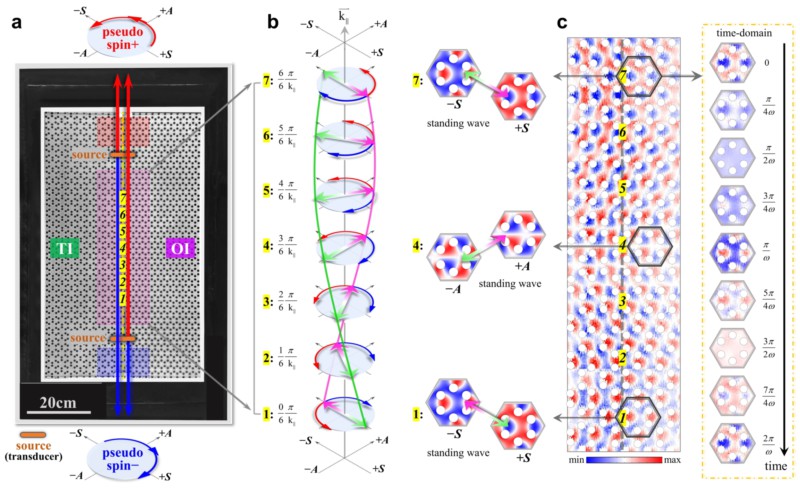
图6，固体声波拓扑绝缘体边界上呈现出的纯自旋流（pure spin current）：a 实验构架为在直波导（拓扑边界）中放置上下两个声源，各自分别向上、下两个方向同时激发具有“自旋-动量锁定”的传输态；b在两个声源的中间区域，即同时存在有两种“赝自旋”对应的、能流相反、振幅一致的固体声波。c实验测量到的该区域内的固体声场分布：可见这一区域中声场的总能流虽然为零，却存在一个在空间上延着边界呈螺旋性的赝自旋传输。

同时，研究团队利用激光干涉测量的方式对固体声波的声场进行了高分辨率检测，首次从实验观测到了玻色子系统——光/声子赝自旋态的展现形式及其演化特征，并进一步证实了拓扑绝缘体独特的“自旋-动量锁定”的螺旋边界态（helical edge state），以及边界上的纯自旋流（pure spin current），为理解玻色子、费米子系统的拓扑性质和与自旋（或赝自旋）相关的传输行为提供了可视化的物理图像。

37000cm威尼斯的余思远副研究员及何程副教授是该论文的共同第一作者；卢明辉教授、刘晓平教授、陈延峰教授为该论文的共同通讯作者。37000cm威尼斯的王振、刘富康、孙晓晨博士、李政博士及南方科技大学的卢海舟教授共同参与了该课题的研究。研究得到了科技部国家重点研发计划、国家自然科学基金委、中组部青年等项目的支持。

（现代工程与应用科学学院 科学技术处）

参考文献：

Lu, L., Joannopoulos, J. D. & Soljacic, M. Topological photonics. Nature Photon. 8, 821-829 (2014). Khanikaev, A. B., & Shvets, G. Two-dimensional topological photonics. Nature Photon. 11, 763 (2017). Huber, S. D. Topological mechanics. Nature Phys. 12, 621-623 (2016). Ge, H., et al. Breaking the barriers: advances in acoustic functional materials. National Science Review 5(2), 159-182 (2017). Bahari, B., Ndao, A., Vallini, F., El Amili, A., Fainman, Y., & Kanté, B. Nonreciprocal lasing in topological cavities of arbitrary geometries, Science 358, 636–640 (2017). Harari, G., Bandres, M. A., Lumer, Y., Rechtsman, M. C., Chong, Y. D., Khajavikhan, M., ... & Segev, M. Topological insulator laser: Theory. Science 359, 1230 (2018). Bandres, M. A., Wittek, S., Harari, G., Parto, M., Ren, J., Segev, M., ... & Khajavikhan, M. Topological insulator laser: Experiments. Science 359, 1231 (2018). Wang, P., Lu, L., & Bertoldi, K. Topological phononic crystals with one-way elastic edge waves. Phys. Rev. Lett. 115, 104302 (2015). Mousavi, S. H., Khanikaev, A. B. &Wang, Z. Topologically protected elastic waves in phononic metamaterials. Nat. Commun. 6, 9682 (2015). Wu, L.-H. & Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 114, 223901 (2015). Chen, Z.-G., et al. Accidental degeneracy of double Dirac cones in a phononic crystal. Sci. Rep. 4, 4613 (2014).